在簡單迴歸中,如果依變數Y是二元型別(是/否;有/無),這時候有著厲害名字的羅吉斯迴歸分析(Logistic regression)是很常使用的演算法。
聽到這種有名字又很長的都是什麼亞洲天王天后的,很想把頭塞進被窩躲起來,好,人生就是挑戰不斷,星期六早上不跑步來複習羅吉斯迴歸分析的使用。
孫子兵法:
敵近而靜者,恃其險也;遠而挑戰者,欲人之進也。
羅吉斯迴歸分析也是屬於監督式學習(Supervised Learning),在執行分析前,我們可能需要將標準答案整理成0~1的數值,0表示 否/不同意,1表示 是/同意;執行羅吉斯迴歸分析後,方程式會回傳依變數Y的成功機率,越接近0表示Y成功機會小,越接近1時則表示成功機會很大。
我們在資料夾MyR新增一支Day24.R
信用卡(creditcard)是一種無擔保的放款,實際也有倒帳(bad debts)風險,因此金融機構的授管單位會依照風險可能來評估是否核准這張卡片的申請。通常授信會依照信用評分、聯徵紀錄及經驗法則共同決定,評分可能會透過評分卡系統依照各種事前的專家經驗或是資料探勘分析結果的權數給分。分數的使用範圍很廣,可以用來給予是否核准卡片、信用額度的高低甚至持卡人差別利率的定價。
因為從事金融產業,也想找信用卡是否核准的資料集,作簡單的機器學習練習。
好!我們會安裝並載入一個之前沒使用過的Package:AER(Applied Econometrics with R),AER剛好內建了一個大約有1,319筆資料的creditcard資料集。
install.packages("AER")
library(AER)
#(1)載入creditcard資料集(包含1,319筆觀察測試,共有12個變數)
data(CreditCard)
#觀察資料欄位
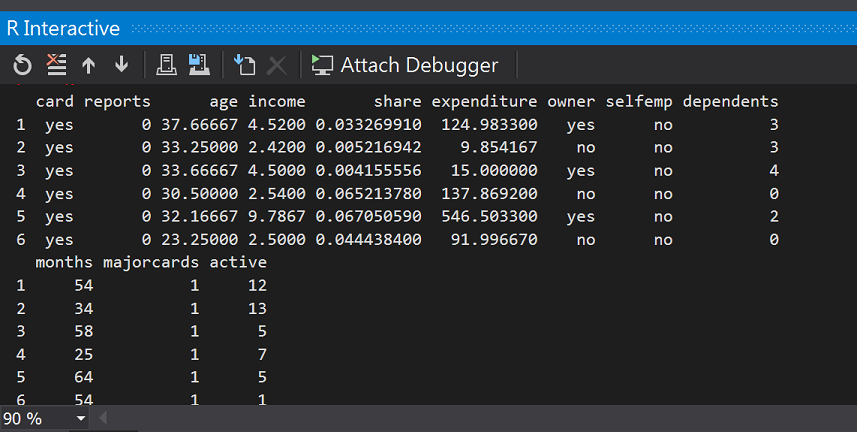
head(CreditCard)
#假設我們只要以下欄位(card:是否核准卡片、信用貶弱報告數、年齡、收入(美金)、自有住宅狀況、往來時間)
bankcard <- subset(CreditCard, select = c(card, reports, age, income, owner,months))
#將是否核准卡片轉換為0/1數值
bankcard$card <- ifelse(bankcard$card == "yes", 1, 0);
假設我們認為信用貶弱報告數(reports)、年齡(age)、收入(imcome)、自有住宅狀況(owners)、往來時間(month)影響Y是否核准卡片(二元型別)!
這時候就很適合羅吉斯迴歸分析!但要注意Y值的範圍 0< Y <= 1 ,所以程式我們先簡單整理。
有關creditcard的欄位介紹 https://rdrr.io/cran/AER/man/CreditCard.html
我們想試著預測兩個信用卡申請件的核准與否:
有信用不良紀錄,收入5萬美金,無自有住宅,往來50個月。#(2)跑羅吉斯模型
card_glm <- glm(formula = card ~ ., family = "binomial", data = bankcard)
#(3)單筆資料預測
#30歲無信用不良紀錄,收入10萬美金,有自有住宅
new <- data.frame(reports = 0, age = 30, income = 10, owner = "yes", months = 50)
result <- predict(card_glm, newdata = new, type = "response")
result
#30歲有信用不良紀錄,收入5萬美金,無自有住宅
new <- data.frame(reports = 1, age = 30, income = 5, owner = "no", months = 50)
result <- predict(card_glm, newdata = new, type = "response")
result
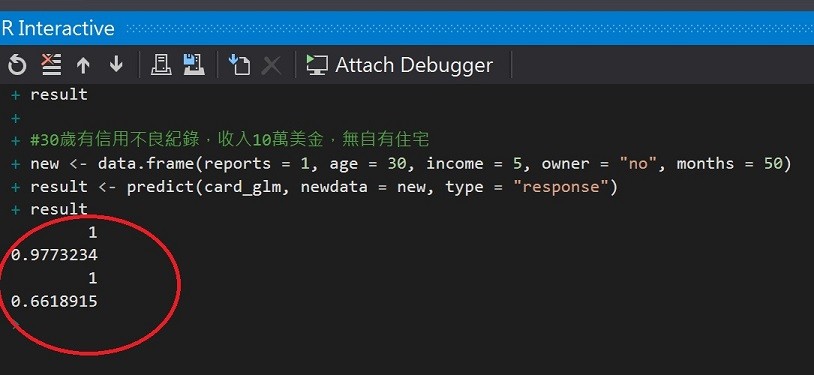
第一件申請核准成功的率97%,第二件則為66%。也許金融機構可能就會對於第二件申請要求補件(補充其他財力證明)或是婉拒申請了。
上面的方式剛好沒經過回測就使用模型的範例,當我們在訓練模型時,如果想要很快取得模型貼近真實模擬的正確率(回測) ,我們可以將觀測出的樣本直接分為2組進行樣本外測試(out of sample test)。我們來將收集到的資料簡單分成測試組及訓練組。
#(4)測試模型
#將資料分為訓練與測試組
#取得總筆數
n <- nrow(bankcard)
#設定隨機數種子
set.seed(1117)
#將數據順序重新排列
newbankcard <- bankcard[sample(n),]
#取出樣本數的idx
t_idx <- sample(seq_len(n), size = round(0.7 * n))
#訓練資料與測試資料比例: 70%建模,30%驗證
traindata <- newbankcard[t_idx,]
testdata <- newbankcard[ - t_idx,]
分組完成後,我們來重新建模並先使用混淆矩陣(confusion matrix)觀察模型的表現。
羅吉斯迴歸模型的函式就是glm(),預測的函式則是predict()。
# 重新建立羅吉斯迴歸模型
card_glm2 <- glm(formula = card ~ ., family = "binomial", data = traindata)
result <- predict(card_glm2, newdata = testdata, type = "response")
#(5)建立混淆矩陣(confusion matrix)觀察模型表現
#r假設我們認定核準率60%以上才視為核卡,其餘是為拒件或補件
result_Approved <- ifelse(result > 0.6, 1, 0)
cm <- table(testdata$card, result_Approved, dnn = c("實際", "預測"))
cm
執行結果: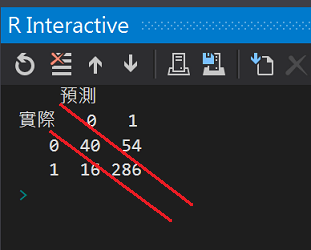
對角線下的就是正確的預測數值,有40個拒件和286個核准件有被模型正確預測。
來計算準確率:
#(6)準確率
#計算核準卡正確率
cm[4] / sum(cm[, 2])
#計算拒補件正確率
cm[1] / sum(cm[, 1])
#整體準確率(對角線元素總和/所有觀察值總和)
accuracy <- sum(diag(cm)) / sum(cm)
accuracy
執行結果: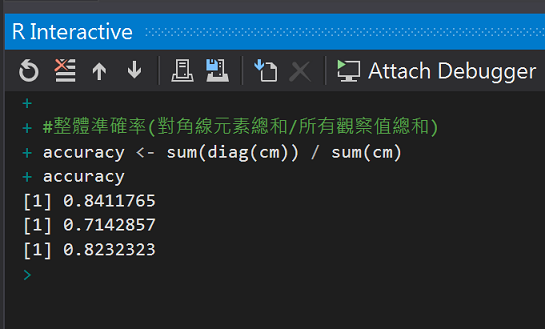
除了準確率的機率數字外,還有一種曲線可以用圖解模型的表現。在繪製ROC曲線前,我們先簡單了解兩個技術名詞TPR(true positive rate)及FPR(false positive rate)。
依據剛剛的數字,這次模型的命中率約84%,但假警報率29%。
回到ROC曲線,曲線主要是由兩個變參數**(1-specificity)及Sensitivity**繪製。
好!來畫ROC曲線,
#畫ROC曲線
library("ROCR")
pred <- prediction(result, testdata$card)
perf <- performance(pred, measure = "tpr", x.measure = "fpr")
#計算AUC
auc <- performance(pred, "auc")
#畫圖
plot(perf, col = rainbow(7), main = "ROC curve", xlab = "Specificity(FPR)", ylab = "Sensitivity(TPR)")
#AUC = 0.5
abline(0, 1)
#實際AUC值
text(0.5, 0.5, as.character(auc@y.values[[1]]))
執行結果:
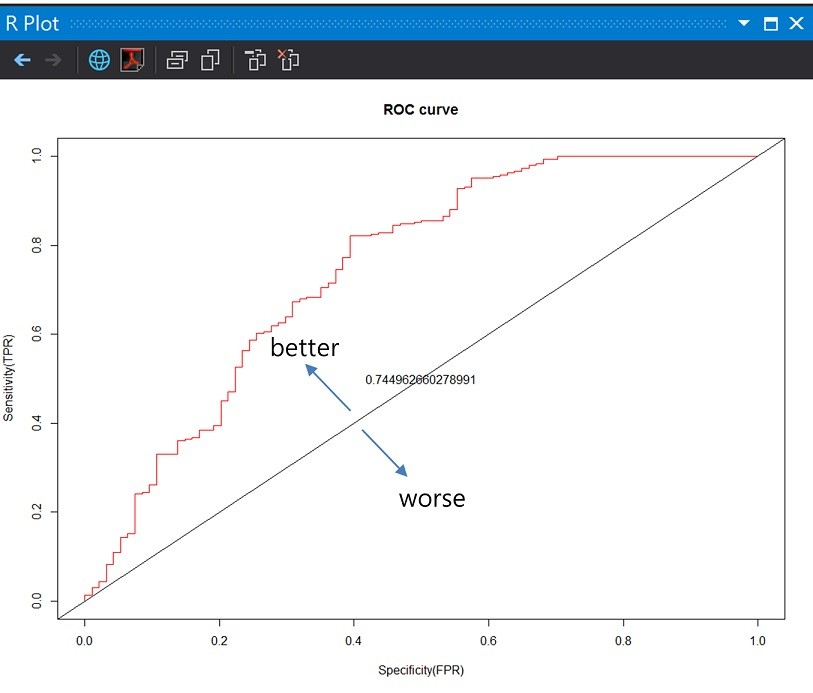
ROC曲線下方的面積稱為AUC(Area under the Curve of ROC)
中間的直線就是AUC=0.5,模型的AUC值越高,正確率越高,由於這次模型的假警報率不低,實際計算出來的AUC=0.74只能算是普普通通的表現。
嚴格說起來她算是分類演算法事務所的藝人,但藝名既然多冠上了迴歸,我們就把她列在迴歸分析的第二個複習菜單,下個菜單,我們將邁向預測Y值是一個連續數值的複迴歸。
另外一份台灣中華大學貢獻到UC Irvine Machine Learning Repository(UCI)的信用卡資料集
http://archive.ics.uci.edu/ml/datasets/default+of+credit+card+clients
隆達鬥牛場
2014.10攝於Ronda,spain
